[证毕QED]一个积分六个平均数
参考文献: Chen, Hongwei. “Means Generated by an Integral.” Mathematics Magazine, vol. 78, no. 5, 2005, pp. 397–99.
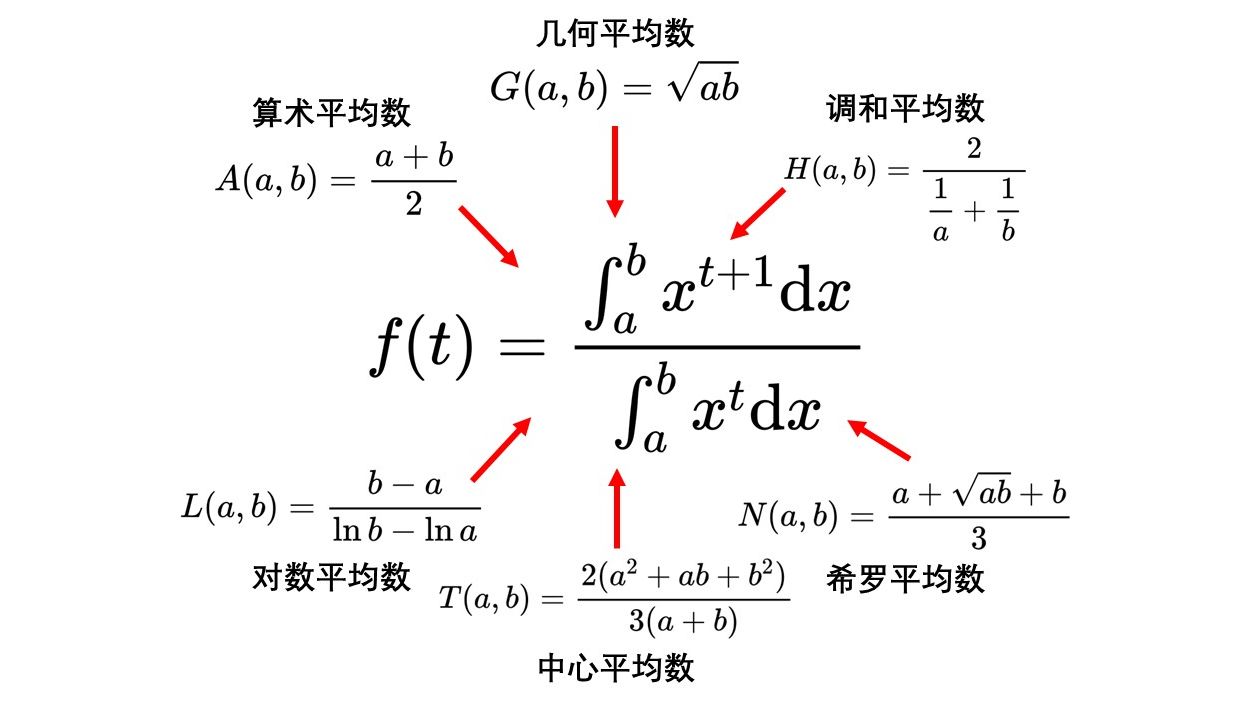
算术平均数A(a,b)=2a+b对数平均数L(a,b)=lnb−lnab−a几何平均数G(a,b)=ab中心平均数T(a,b)=3(a+b)2(a2+ab+b2)调和平均数H(a,b)=a1+b11希罗平均数N(a,b)=3a+ab+b
↓
f(t)=∫abxtdx∫abxt+1dx
L(a,b)=lnb−lnab−a=(lnx)∣abx∣ab=∫abx1 dx∫ab dx=∫abx−1 dx∫abx0 dx=f(−1)
A(a,b)=2b+a=2(b−a)(b+a)(b−a)=2(b−a)b2−a2=x∣ab21x2ab=∫ab dx∫abx dx=∫abx0 dx∫abx1 dx=f(0)
H(a,b)=b1+a12=(b1+a1)(b1−a1)2(b1−a1)=21(b21−a21)b1−a1=−21x−2ab−x−1ab=∫abx−3 dx∫abx−2 dx=f(−3)
G(a,b)=ab=abb−ab−a=a1−b1b−a=−2x−21ab2x21ab=∫abx−23 dx∫abx−21 dx=f(−23)
T(a,b)=3(a+b)2(a2+ab+b2)=3(b2−a2)2(b3−a3)=21x2ab31x3ab=∫abx dx∫abx2 dx=f(1)
N(a,b)=3a+ab+b=2(b21−a21)32(b23−a23)=2x21ab32x23ab=∫abx−21 dx∫abx21 dx=f(−21)
调和平均数f(−3)=H(a,b)=a1+b11对数平均数f(−1)=L(a,b)=lnb−lnab−a算术平均数f(0)=A(a,b)=2a+b几何平均数f(−23)=G(a,b)=ab希罗平均数f(−21)=N(a,b)=3a+ab+b中心平均数f(1)=T(a,b)=3(a+b)2(a2+ab+b2)
在 b>a>0 时, f(t) 在 R 上单调递增, 且 t→−∞limf(t)=a, t→∞limf(t)=b.
H(a,b)≤G(a,b)≤L(a,b)≤N(a,b)≤A(a,b)≤T(a,b)

t=2